
| Beautiful Buildings Peter Landshoff, Chairman of the Clarkson Road Working Group |
This striking photograph was taken by Professor Geoffrey Grimmett who, on a sunny day in December, climbed up the contractor?s crane. On the right in the foreground is the Statistical Laboratory, in which Geoffrey has been working since it was completed in April. The building behind it was occupied by pure mathematicians last August, and the double building at the back is the Märit and Hans Rausing, which was the first building to be completed in January 2000 and is mostly for theoretical physics.
 |
The low building on the left has a grass roof. The Centre for Mathematical Sciences is in a residential area and the City planners rightly demanded that the site be as `green' as possible. So we have a pleasant garden on the roof on which we can walk and which allows us easily to pass between the pavilions that surround it. Easy communication was an important feature of the design concept and is so very important for stimulating interactions among mathematical scientists so as to help them to get creative ideas. For this reason the coffee room/cafeteria beneath the grass roof plays a key role in the production of world-leading research.
Just beneath the crane, and not seen in the figure, the pavilion that will house the Faulkes Institute for Geometry is nearing completion, and next to it the Betty and Gordon Moore Library. The Library will open on 1 October and will be the University?s new library for the physical sciences, technology and mathematics. The development will be completed by three further pavilions, which are just about to begin construction along the left of the photograph.
So everything will be finished by early 2003. We hope that by then too we will have closed the funding gap, which now stands at about 2% of the 60 million pound total cost of the project. If you can help, please contact:
| Patrick Hawke-Smith | For North America: Cambridge in America |
|
|
|---|---|---|---|
| Cambridge University Development Office 10 Trumpington Street Cambridge CB2 1QA UK |
708 Third Avenue 14th Floor New York NY 10017 USA |
||
| telephone: +44 (0)1223 339982 fax: +44 (0)1223 460817 email: ph250@cam.ac.uk |
telephone: +1 212 984 0960 fax: +1 212 984 0970 |
| The Isaac Newton Institute Robert Hunt, Deputy Director |
The Isaac Newton Institute, situated in the south-east corner of the Clarkson Road site, has the distinction of being the oldest building on the site: opened in July 1992 it has now reached the grand old age of eight. It is the UK?s National Research Institute for the Mathematical Sciences. The recent munificence of Dr Dill Faulkes has enabled the building of the Faulkes Gatehouse, which as well as providing a formal entrance to the Centre for Mathematical Sciences will provide the Newton Institute with much-needed state-of-the-art seminar space and extra offices.
 |
The main activity of the Institute is to run visitor programmes, on particular topics, typically lasting for four or six months. These programmes attract the most eminent experts in the field from around the world, and benefit the entire UK mathematics community by bringing international visitors together with those from the UK to work intensively on the chosen topic. Many of the most prominent visitors stay for several months, while the Institute always welcomes others who wish to visit just for a specific week-long workshop or even a single seminar! In total the Institute attracts around 1600 visitors each year.
The topics for Institute programmes are carefully chosen by its Scientific Steering Committee, a panel of eminent British and international mathematicians. The themes are chosen from the whole range of the "Mathematical Sciences", interpreted in its very widest sense to include the full range of scientific subjects to which mathematics may be applied (which is to say, practically all of them). Interdisciplinarity is an important consideration for the Committee, and a high proportion of the chosen topics cut across two, three or often more different subject areas. Another important consideration is timeliness: each programme should come at a time when the topic is ripe for new discoveries rather than being in a consolidation phase.
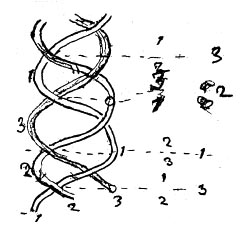
There are (at the time of writing, December 2000) two programmes currently running at the Newton Institute. The first, Singularity Theory, studies in a generic way the singularities that arise in a wide range of mathematics and mathematical models (such as in geometry, in optics, in relativity and cosmology, in the study of cracks in materials, and innumerable others). Although, given its wide application, singularity theory is clearly of fundamental importance, it is underdeveloped as a mathematical discipline, and this programme has helped to redress that. The second programme, Geometry and Topology of Fluid Flows, is concerned with the way in which geometrical concepts, such as knots and braids, can govern the behaviour of complex fluid flows (by which we mean either liquid or gaseous flows), especially when magnetic fields are present. This idea in itself is far from new - Lord Kelvin was well aware of the principle over a century ago, as the diagram in his notebook shows (see figure 1) - but the concept was not really developed until the 1970s onwards when its relevance to thermonuclear fusion and astrophysics began to become clear. More recently, numerous other applications have been discovered, such as in chemical systems (e.g., long knotted polymer chains) and biology (knotted DNA strands, which may be linked to some genetic disorders). The basic problem can be illustrated by solar flares and other structures in the Sun?s corona (see figure 2): magnetic field lines within the corona intertwine, and the mathematical complexity of the knot is a good way of estimating the energy stored in the structure.
 |
 |
| Figure 1: Sketch of three vortices interlaced to form a braid. Notebook 55, papers of Lord Kelvin, unpublished drawing. Courtesy of the Syndics of Cambridge University Library. | Figure 2: Prominences are huge clouds of relatively cool dense plasma suspended in the Sun's hot, thin corona. At times, they can erupt, revealing the interwined magnetic field structure. Courtesy of NASA. |
The Newton Institute programme has allowed more than 100 participants from across the world (over 20 countries) to meet and interact for an extended period under one roof. As one of the organisers of the programme says, "the architecture of the building really works: it provides a ?market square? for the interchange of ideas." It is pleasing that the new pavilions on the Clarkson Road site have taken so much of their basic design from the successful "experiment" of the Institute, in terms of their layout with all its opportunities for interaction. The coffee rooms, cafeteria and circulation areas in the new buildings were modelled on those in the Institute - these are the most important places for mathematicians as a lot of new ideas are generated there, so they were designed first!
One major area of current research that has been studied and advanced during the programme is the concept of an "ideal knot" in the context of magnetic flux. One way of visualising this concept is to imagine a long thin balloon, of the type used by balloon modellers to create giraffes and dogs, which represents a magnetic flux tube - that is to say, the magnetic field lines run along the length of the balloon. Tie this balloon loosely along its length in a knot, representing a knotted flux tube (see figure 3). Now flux tubes prefer to "relax", that is to minimise their energy; but as they do so they must conserve their volume so that the cross-sectional area grows as the length decreases. If you imagine this process you will see that there comes a point when the tube can relax no more (when the sides of the balloon have started to touch each other), and this represents the "ideal knot" - the configuration which a real flux tube adopts in equilibrium.
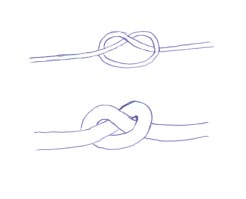 |
| Figure 3 |
Recently, a problem being worked on by both of the current programmes - the so-called "finite-time singularity in the Navier-Stokes equation" problem - has become one of seven "Millennium Prize Problems" for which the Clay Mathematics Institute in Cambridge MA, USA, has off052:57 PM 6/21/01ered $1 million for a proof. Naturally the Newton Institute had no knowledge when it planned these programmes that the prize would be offered, but it is reassuring to see that the Institute has anticipated the world?s interest.
 |
| The Faulkes Gatehouse, which will become the main pedestrian entrance to the site and provide valuable extra accommodation for the Newton Institute, will be ready for topping out on 19 February. |
| Part III in Cambridge Frederic Pauquay, overseas student, Faculty of Mathematics |
Coming to Cambridge is, for an overseas student, an experience that changes both ones life and the way one looks at things. In almost all respects, Cambridge is not representative of Great Britain and is much more like a microcosm of its own: on the scientific and cultural side, it is the most active and stimulating environment I have ever lived in, but on the other hand, Cambridge is a place where tradition lives on and numerous features, such as the collegiate system, have been inherited from its medieval origins. Therefore, it will not come as a surprise to learn that the subtleties of the Cambridge system are, at the beginning, quite difficult to get used to for newcomers, especially if they are foreigners.
When I finished my first degree in physics, my previous university was the only scientific world I knew and I saw no reason to move to another university to do my PhD. But, my former supervisor, a well-travelled man, insisted that the world is bigger, with many good places: he was particularly keen for me to try a university town in England called Cambridge, which is not exactly all about rowing, high living and excess... For a physicist, Cambridge means Newton, Maxwell, Dirac and many others who made their mark in science. Alongside its worldwide reputation, I was attracted to Cambridge by noticing how often the address appears on papers in leading journals like the Physical Review. As a consequence, I eventually decided Cambridge was the place where I wanted to go and I started the journey that I hoped would lead me to a research studentship at the University of Cambridge, Department of Applied and Theoretical Physics (DAMTP).
After I had passed the English proficiency test and been admitted to a college, the next step was Part III: in most handbooks or prospectuses on postgraduate studies in Cambridge, this one year taught course is presented as the usual route to becoming a PhD student in DAMTP and a way of assessing potential research students on the grounds of their performance in Part III exams. As I later realised, Part III is actually much more than that; undergraduate courses usually cover the physics and mathematics that have been discovered until 1940 or so and the gap one has to fill to get to the research level in a particular field continuously increases. Part III provides a wide range of optional advanced courses and gives students an overview of the current research being carried out together with the knowledge necessary to start doing research in the domain they are interested in. All in all, Part III was an enjoyable and interesting experience even though the intensive week of examinations that put an end to it left many students like zombies.
Now, I am in my first year of PhD and life is very different: it is less stressful but still very interesting. I consider myself very lucky to work in a large department like DAMTP where one can interact with talented people from lots of different backgrounds and exchange ideas.
| The David Crighton Fund |
 |
| We invite you to help establish a fund in memory of David Crighton to support young researchers in his field |
The UK and international applied mathematics communities have been sadly shocked by the early death on 12 April 2000 of David Crighton, Professor of Applied Mathematics at the University of Cambridge, Head of the Department of Applied Mathematics and Theoretical Physics, and Master of Jesus College. David was cruelly struck by cancer early in 1999, when at the height of his powers; in the face of increasing difficulties, and to the immense admiration of his friends and colleagues, he continued to work at full stretch, relinquishing none of his heavy responsibilities, until just two weeks before his death. David Crighton was an unusually influential figure not only within Cambridge but also in many spheres of national and international activity. He was President of the Institute of Mathematics and its Applications from 1996 to 1999, and was President-Elect of the London Mathematical Society at the time of his death. In 1996 he took over from the late George Batchelor the editorship of the Journal of Fluid Mechanics, the leading journal in the field. He also took over from Batchelor the chairmanship of EUROMECH, the European mechanics organisation, and transformed it into a Society of which he was the first President (and still Vice-President at the time of his death). He involved himself deeply in enhancing mathematical education at all levels. On top of all that he had an active research career too.
David?s research achievements were in the fields of linear and nonlinear wave theory, of aeroacoustics, and of aeroelasticity in which there is strong coupling between fluid flow and the vibration of solid boundaries. His work had important application to the generation of sound and vibration by underwater structures and to making aeroplane engines quieter. He also wrote seminal papers on intense sound waves, on the manner in which shock waves develop when they propagate over large distances; and on the phenomenon of ?Anderson localisation? whereby wave disturbances in the neighbourhood of periodic structures can remain trapped near the region of excitation.
David played an enthusiastic leading role in the fundraising and the design work for the University?s stunning new Centre for Mathematical Sciences. By combining and developing elements that are at present a mile apart, the Centre creates a concentration of the mathematical sciences whose strength and diversity rivals any in the world.
David Crighton provided advice, encouragement and stimulation to many young researchers. We would therefore like to commemorate David?s outstanding service both to the University of Cambridge and to the wider UK and international applied mathematics communities, by establishing a David Crighton Fund, the income from which will be used to provide support for young research workers (graduate students and postdoctoral fellows) in the area of fluid dynamics.
Many in the world of applied mathematics will have been touched by David?s warmth of character, his great good humour, his caring personality, his boundless energy and enthusiasm, and his exceptional devotion both to research and to the dissemination of knowledge at all levels. We hope that this will be a fitting memorial, and that those who have known David will wish to respond generously.
| UK and other non-US donors - if you would like to support the David Crighton Fund, please contact: Patrick Hawke-Smith, Cambridge University Development Office, 10 Trumpington Street, Cambridge CB2 1QA, UK. UK income tax / capital gains tax payers - please note that your donation can be made under the Gift Aid scheme, increasing its value by 28% at no additional cost to you. US donors - please send your donation, made payable to CUDOUS, to The Cambridge University Development Office in the United States (a section 501(c)(3) organisation) at: CUDOUS, 708 Third Avenue, 14th Floor, New York, NY 10017, USA. |
